Sixth Summer School on Computer Vision, Graphics and Image Processing

Machine Learning Algorithms Session 2 (b)

Avisek Gupta (avisek003@gmail.com)

Electronics and Communication Sciences Unit

June 04, 2019

Supervised Learning

  • Classification: Learn to predict a class / category

  • Regression: Learn to predict a target real value

Linear Regression:

Find the line that best fits the given data

In [2]:
import numpy as np
import matplotlib.pyplot as plt


data = np.array([
    [0.20, 0.30], [0.32, 0.23], [0.39, 0.35], [0.46, 0.42], 
    [0.51, 0.39], [0.60, 0.47], [0.64, 0.51], [0.75, 0.46]
])


plt.figure()
plt.scatter(data[:,0], data[:,1], marker='o', c='C0')
plt.plot([0.1, 0.9], [0.174251 + 0.1*0.448577, 0.174251 + 0.9*0.448577], c='C1', linestyle=':', linewidth=1)
plt.show()

Linear Regression:

1. Regression Model: A straight line $y = w_0 + w_1 x $ .

2. Learning: Given a regression model, estimate the parameters ($w_0, w_1$) of the model.

3. Cost Function:

  • Measures how "bad" the model is.

  • Used to guide the selection of better model parameters.

Example of a Cost Function:

Mean Squared Error (MSE) = $\frac{1}{n} \sum_{i=1}^{n} (y_i - (w_0 + w_1 x_i))^2$

In [3]:
import numpy as np
import matplotlib.pyplot as plt


data = np.array([
    [0.20, 0.30], [0.32, 0.23], [0.39, 0.35], [0.46, 0.42], 
    [0.51, 0.39], [0.60, 0.47], [0.64, 0.51], [0.75, 0.46]
])
x = data[:,0]
y = data[:,1]


random_w = np.random.rand(2)

mse = np.mean((y - (random_w[0] + random_w[1] * x)) ** 2)
print('MSE =', mse)


plt.figure()
plt.scatter(data[:,0], data[:,1], marker='o', c='C0')
plt.plot([0.1, 0.9], [random_w[0] + 0.1*random_w[1], random_w[0] + 0.9*random_w[1]], c='C1')
plt.show()

MSE = 0.13185507918320447

Linear Regression:

1. Regression Model: A straight line $y = w_0 + w_1 x $ .

2. Learning: Given a regression model, estimate the parameters ($w_0, w_1$) of the model.

3. Cost Function:

  • Measures how "bad" the model is.

  • Used to guide the selection of better model parameters.

4. Optimization Algorithm:

  • Estimates the model parameters by trying to reduce the cost function.

  • There can be many possible ways to optimize the same cost function.

Example of an Optimization Algorithm: Gradient Descent

Gradient Descent to optimize a function $f(w)$:

1. Pick a random initital point $w_0$

2. Loop till convergence: $w_{i+1} := w_{i} - \alpha \nabla f(w_{i})$

($\alpha$: Step size)

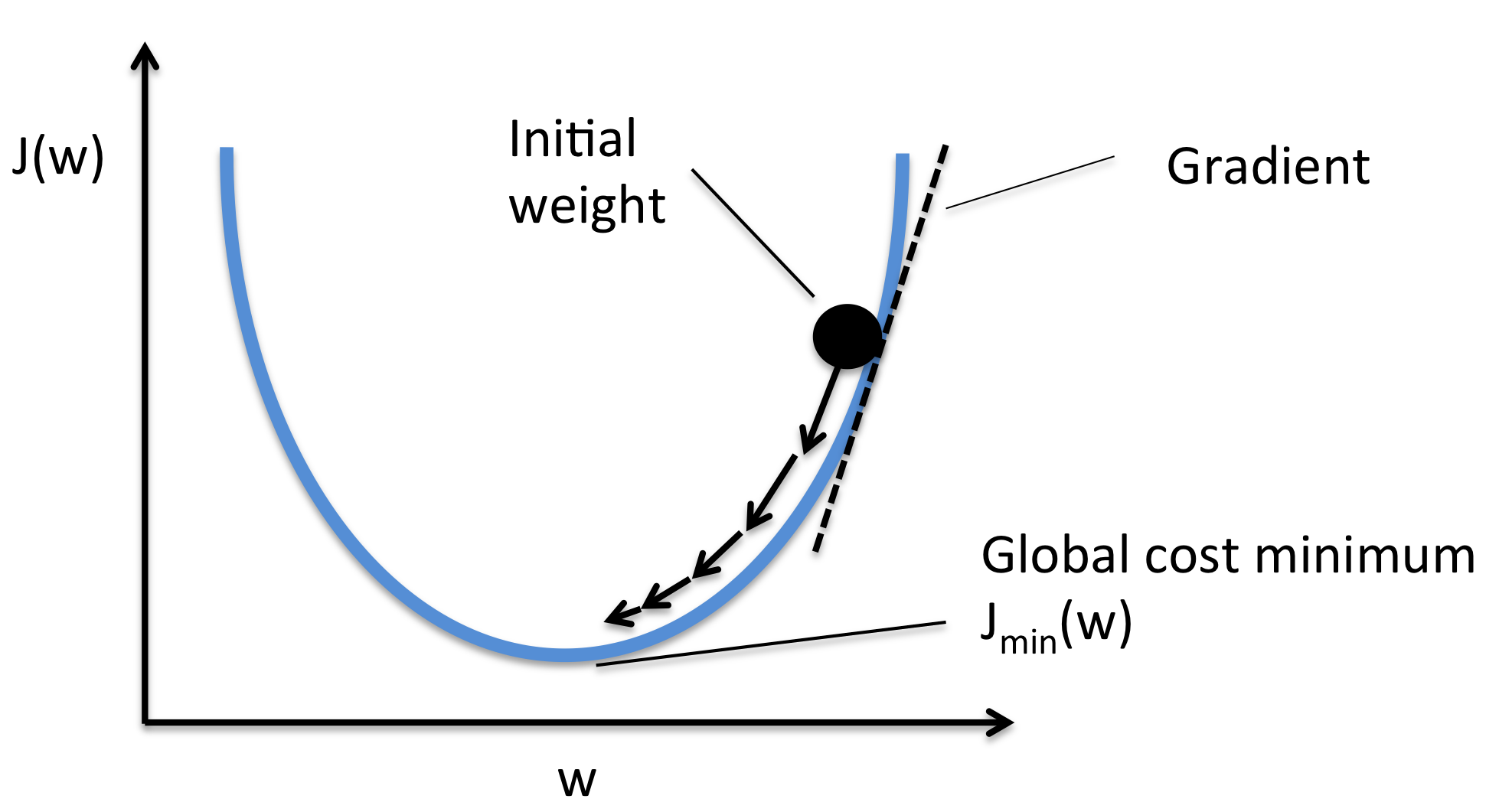
Source: https://rasbt.github.io/mlxtend/user_guide/general_concepts/gradient-optimization/

Example: Gradient Descent of a simple function $f(w) = w^2+4$

Conjugate Gradient Descent: Automatically selects an appropriate step size

In [2]:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize


def fun1(w):
    return (w ** 2) + 4

def grad_fun1(w):
    return 2 * w


w0 = (np.random.rand() * 20) - 10
print('Initial Guess =', w0)

res = minimize(fun=fun1, jac=grad_fun1, x0=w0, method='CG')


print(res)
print('---------------------')
print('Solution =', res.x)
print('Objective Function Value =', res.fun)


plt.figure(dpi=90)
x = np.linspace(-10, 10, 100)
plt.plot(x, fun1(x), c='gray')
plt.scatter(w0, fun1(w0), c='y', marker='o', s=60)
plt.scatter(res.x, res.fun, c='r', marker='x', s=80)
plt.show()

Initial Guess = 4.851063961810411
     fun: 4.0
     jac: array([1.77635684e-15])
 message: 'Optimization terminated successfully.'
    nfev: 3
     nit: 1
    njev: 3
  status: 0
 success: True
       x: array([8.8817842e-16])
---------------------
Solution = [8.8817842e-16]
Objective Function Value = 4.0

Linear Regression:

1. Regression Model: A straight line $y = w_0 + w_1 x $ .

2. Learning: Given a regression model, estimate the parameters ($w_0, w_1$) of the model.

3. Cost Function: MSE

4. Optimization Algorithm: Gradient Descent

In [3]:
import numpy as np
import matplotlib.pyplot as plt


data = np.array([
    [0.20, 0.30], [0.32, 0.23], [0.39, 0.35], [0.46, 0.42], 
    [0.51, 0.39], [0.60, 0.47], [0.64, 0.51], [0.75, 0.46]
])
X = np.hstack((np.ones((data.shape[0], 1)), np.reshape(data[:,0], (data.shape[0], 1))))
y = data[:,1]


def mse(w):
    # Implement MSE
    return np.mean((y - (X @ w)) ** 2)

def grad_mse(w):
    # Implement the gradient of MSE
    return 2 * np.mean(np.reshape(y - (X @ w), (X.shape[0], 1)) * (-X), axis=0)

w0 = np.random.rand(X.shape[1])
print('Initial Guess w0 =', w0)
print('MSE at w0 =', mse(w0))
# Gradient Descent to get w1 and w0
res = minimize(fun=mse, jac=grad_mse, x0=w0, method='CG')

w = res.x
print('Final w =', w)
print('Final MSE =', mse(w))
plt.figure()
plt.scatter(data[:,0], data[:,1], marker='o', c='gray')
plt.plot(
    np.array([data[:,0].min()-0.2,data[:,0].max()+0.2]), 
    w[1] * np.array([data[:,0].min()-0.2,data[:,0].max()+0.2]) + w[0], c='r'
)
plt.show()

Initial Guess w0 = [0.57454579 0.62604719]
MSE at w0 = 0.23927526047729206
Final w = [0.17426561 0.4485485 ]
Final MSE = 0.0020467201122117825

How Model Complexity affects Generalization Error

Regression Example: Polynomial Regression

Regression Model: A degree 'd' polynomial curve $y = w_0 + w_1 x + w_2 x^2 + ... + w_d x^d$

Degree-2 Polynomial Regression

In [4]:
import numpy as np
import matplotlib.pyplot as plt


data = np.array([ [0.20, 0.30], [0.32, 0.23], [0.39, 0.35], [0.46, 0.42], 
    [0.51, 0.39], [0.60, 0.47], [0.64, 0.51], [0.75, 0.46] ])
x = np.reshape(data[:,0], (data.shape[0], 1))
X = np.hstack((x, x ** 2))
y = data[:,1]


from sklearn import linear_model
reg = linear_model.LinearRegression().fit(X, y)
w = np.hstack(([reg.intercept_], reg.coef_))


X = np.hstack((np.ones((data.shape[0], 1)), X))
print('Final w =', w)
print('Final MSE =', mse(w))
plt.figure()
plt.scatter(X[:,1], y, marker='o', c='gray')
plt.plot(X[:,1], np.dot(X, w), c='r')
plt.show()

Final w = [ 0.13015947  0.66069144 -0.22310993]
Final MSE = 0.0020054996464536454

Degree-4 Polynomial Regression

In [5]:
import numpy as np
import matplotlib.pyplot as plt


data = np.array([ [0.20, 0.30], [0.32, 0.23], [0.39, 0.35], [0.46, 0.42], 
    [0.51, 0.39], [0.60, 0.47], [0.64, 0.51], [0.75, 0.46] ])
x = np.reshape(data[:,0], (data.shape[0], 1))
X = np.hstack((x, x ** 2, x ** 3, x ** 4))
y = data[:,1]


from sklearn import linear_model
reg = linear_model.LinearRegression().fit(X, y)
w = np.hstack(([reg.intercept_], reg.coef_))


X = np.hstack((np.ones((data.shape[0], 1)), X))
print('Final w =', w)
print('Final MSE =', mse(w))
plt.figure()
plt.scatter(X[:,1], y, marker='o', c='gray')
plt.plot(X[:,1], np.dot(X, w), c='r')
plt.show()

Final w = [  1.49762761 -11.97854825  38.76986039 -48.85488009  21.34314688]
Final MSE = 0.0006777706737177815

Degree-7 Polynomial Regression

In [6]:
import numpy as np
import matplotlib.pyplot as plt


data = np.array([ [0.20, 0.30], [0.32, 0.23], [0.39, 0.35], [0.46, 0.42], 
    [0.51, 0.39], [0.60, 0.47], [0.64, 0.51], [0.75, 0.46] ])
x = np.reshape(data[:,0], (data.shape[0], 1))
X = np.hstack((x, x ** 2, x ** 3, x ** 4, x ** 5, x ** 6, x ** 7))
y = data[:,1]


from sklearn import linear_model
reg = linear_model.LinearRegression().fit(X, y)
w = np.hstack(([reg.intercept_], reg.coef_))


X = np.hstack((np.ones((data.shape[0], 1)), X))
print('Final w =', w)
print('Final MSE =', mse(w))
plt.figure()
plt.scatter(X[:,1], y, marker='o', c='gray')
plt.plot(X[:,1], np.dot(X, w), c='r')
plt.show()

Final w = [-1.46792943e+02  2.59466196e+03 -1.88432721e+04  7.32810003e+04
 -1.65354856e+05  2.17150048e+05 -1.54086738e+05  4.56825909e+04]
Final MSE = 3.9294836087641127e-23

Relation between Model Complexity and Generalization Error

Higher Model Complexity -> Higher Chances of "Overfitting" the data -> High Generalization Error

Lower Model Complexity -> Higher Chances of "Underfitting" the data -> High Generalization Error

How can we find the ideal model complexity?

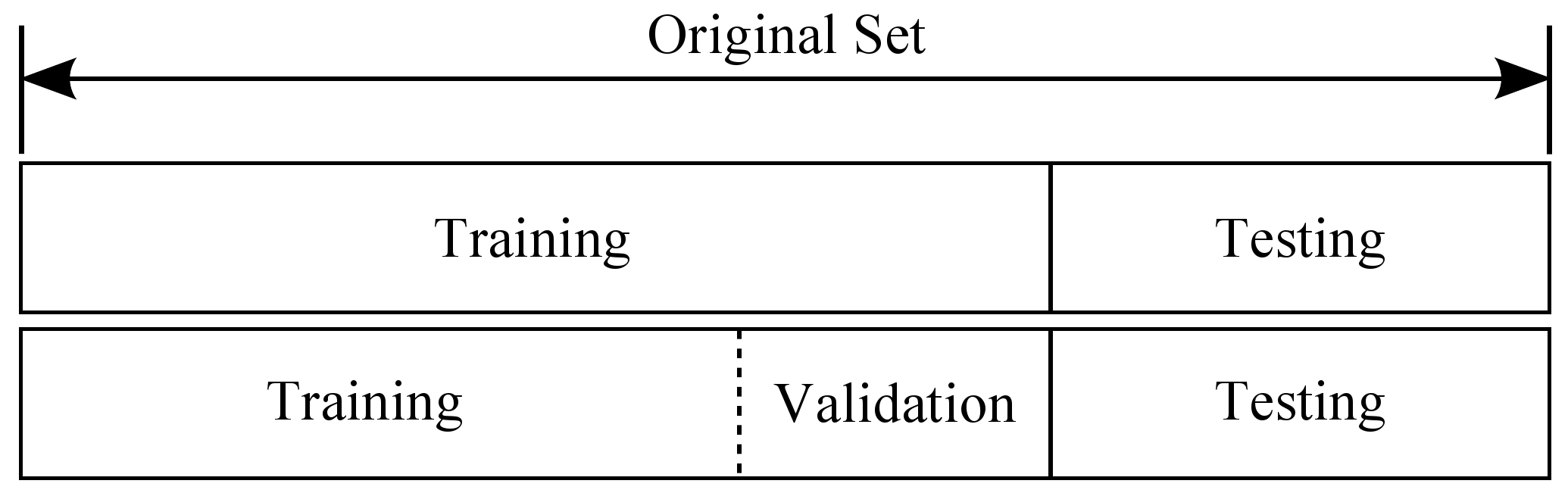
Source: https://rpubs.com/charlydethibault/348566

Divide a data set into three parts. Each part serves different purposes:

1. Use Training Data to estimate model parameters.

2. Use Validation Data to select model complexity.

3. Use Test Data to estimate Generalization Error.

Logistic Regression:

Draw a line between two classes of points.

Let there be two classes: $Y \in \{0,+1\}$

Logistic Function:

$g(x) = \dfrac{1}{1+e^{−w^T x}}$

Source: https://guide.freecodecamp.org/machine-learning/logistic-regression/

1. For points on a line: $w^Tx = 0$, and therefore $g(x) = 0.5$

2. For points on one side of a line: $w^Tx < 0$, and therefore $g(x) \rightarrow 0$

3. For points on one side of a line: $w^Tx > 0$, and therefore $g(x) \rightarrow 1$

1. Logistic Regression Model: A decision boundary $y = g(x) = \dfrac{1}{1+e^{−w^T x}} $ .

2. Learning: Estimate the model parameters $w$.

3. Cost Function: Cross Entropy

$ CE(w) = - \frac{1}{n} \sum_{i=1}^{n} \left\{ y_i \log g(x_i) + (1 − y_i) \log (1 - g(x_i)) \right\}$,

[ The gradient of the objective function is: $\nabla CE(w) = -\frac{1}{n} \sum_{i=1}^{n} (y_i - g(x_i)) x_i$ ]

4. Optimization Algorithm: Gradient Descent

Implementing Logistic Regression:

In [7]:
a1 = np.random.uniform(low=0, high=0.5, size=(100,2))
a2 = np.random.uniform(low=0.5, high=1, size=(100,2))
X = np.hstack((np.ones((200,1)), np.vstack((a1, a2))))
y = np.hstack(( np.zeros((100)), np.ones((100)) ))


def obj_fun(w):
    gx = 1 / (1 + np.exp(-np.dot(X, w)))
    # Implement Cross-Entropy
    return - np.mean((y * np.log(np.fmax(gx, 1e-9))) + ((1 - y) * np.log(np.fmax(1 - gx, 1e-9))))
    
def obj_grad(w):
    gx = 1 / (1 + np.exp(-np.dot(X, w)))
    # Implement the gradient of Cross-Entropy
    return - np.mean(np.reshape((y - gx), (X.shape[0],1)) * X, axis=0)


w0 = np.random.rand(X.shape[1]) * 2 - 1

res = minimize(fun=obj_fun, jac=obj_grad, x0=w0, method='CG')


print('Initial Guess =', w0)
print('Initial Obj Fun val =', obj_fun(w0))
plt.figure()
for i in range(2):
    plt.scatter(X[y==i,1], X[y==i,2], marker='x')
extreme_xvals = np.array([np.min(X[:,1]), np.max(X[:,1])])
plt.plot(extreme_xvals, (-w0[0] - w0[1] * extreme_xvals) / w0[2], c='r')
plt.show()
plt.figure()
for i in range(2):
    plt.scatter(X[y==i,1], X[y==i,2], marker='x')
final_w = res.x
print('Final w =', final_w)
print('Obj Fun val =', obj_fun(final_w))
plt.plot(extreme_xvals, (-final_w[0] - final_w[1] * extreme_xvals) / final_w[2], c='r')
plt.ylim(extreme_xvals+np.array([-0.05, 0.05]))
plt.show()

Initial Guess = [ 0.91838786  0.47885874 -0.55977214]
Initial Obj Fun val = 0.8041478769660253

Final w = [-121.73434637  148.14913794   95.21344292]
Obj Fun val = 2.015633659935192e-05

Application of Logistic Regression: Binary Classification of Handwritten '0's and '1's

In [9]:
from sklearn.datasets import load_digits
X, y = load_digits().data, load_digits().target
X = X[y<2,:]
y = y[y<2]
X = np.hstack((np.ones((X.shape[0],1)), X))
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1)


def obj_fun(w, X, y):
    gx = 1 / (1 + np.exp(-np.dot(X, w)))
    return -np.mean(y * np.log(np.fmax(gx, 1e-6)) + (1 - y) * np.log(np.fmax(1 - gx, 1e-6)))

def obj_grad(w, X, y):
    gx = 1 / (1 + np.exp(-np.dot(X, w)))
    return -np.mean(np.reshape(y - gx, (y.shape[0],1)) * X, axis=0)


min_cost = +np.inf
for i in range(10):
    w0 = (np.random.rand(X.shape[1]) * 2) - 1
    res = minimize(fun=obj_fun, jac=obj_grad, args=(X_train, y_train), x0=w0, method='CG')
    if res.fun < min_cost:
        min_w = res.x
        min_cost = res.fun


from sklearn.metrics import accuracy_score
print('Accuracy =', 
      accuracy_score(y_test, np.round(1 / (1 + np.exp(-np.dot(X_test, min_w)))))
)
for i in range(5):
    plt.figure(dpi=50)
    plt.imshow(np.reshape(X_test[i,1:], (8,8)), cmap='gray')
    plt.xlabel(
        'Predicted Digit: '+str(int(np.round(1 / (1 + np.exp(-np.dot(X_test[i,:], min_w)))))),
    fontsize=24)
    plt.xticks([], [])
    plt.yticks([], [])
    plt.show()

Accuracy = 1.0

References:

scipy.optimize Documentation

Scikit Learn User Guide